Tentatives de résolution

Approche inverse : arbre de Syracuse

Depuis le début, nos approches sont similaires. Nous partons d'une itération sur l'application de Syracuse pour en observer ou démontrer des propriétés. Une autre approche possible est de changer de point de vue et de prendre le problème à l'envers. C'est de cette idée qu'est née l'arbre de syracuse.

Partons de 8 Pour y arriver, nous venons soit de l'application de Syracuse \(3x+1\), soit de \(\displaystyle \frac x 2\).
On tente de résoudre l'équation d'inconnue \(n\in \mathbb N^*\) : \[3n+1=8\iff 3n=7\iff n=\frac{7}{3} \notin \mathbb N^*\] On en déduit donc que 8 ne vient pas de l'application de Syracuse sur les nombres impairs car \(\displaystyle \frac{7}{3}\) n'est pas un entier naturel. Ainsi, 8 vient forcément de l'application de Syracuse sur les nombres pairs et donc de 16.

Nous passons maintenant à 16. Par la même méthode que pour 8, on résoud les équations d'inconnues \(n\in \mathbb N^*\) : \[3n+1=16\iff n=5\in \mathbb N^*\, \, \, \text{ou}\, \frac{n}{2}=16\iff n=32\in \mathbb N^* \] Ces deux équations possèdent des solutions naturelles, l'arbre de Syracuse possède donc 2 branches qui représentent les 2 applications de Syracuse possibles. À partir de ces deux branches, d'autres seront à leur tour crées. Ainsi, il est dit que tous les nombres entiers naturels strictement positifs sont présents dans cet arbre. Personne n'a cependant encore réussi à le démontrer.

Recherche de cycles non triviaux

Une autre approche pour vaincre la conjecture de Syracuse serait de prouver qu'il existe un cycle différent du cycle trivial.
Pour ce faire, raisonnons par l'absurde et admettons qu'il existe un cycle de longueur 3 différent du cycle \((4, 2, 1)\)
Supposons \(A, B,C\in \mathbb N^*\) tel que \(A\lt B\lt C\) et \[A \rightarrow B \rightarrow C \rightarrow A\] Nous avons donc nécessairement \(A\) impair car, le cas échéant, \(A\) serait divisé par 2 et \(B\lt A\).
Ainsi \(B=3A+1\), qui est pair donc \(C=\displaystyle \frac{B}{2}=\frac{3A+1}{2}\). Puisque \(C \to A\) et \(C \gt A\), \(C\) est pair et vaut \(\displaystyle \frac{B}{2}=\frac{1}{2}\left(\frac{3A+1}{2}\right)=\frac{3A+1}{4}\)
Résolvons maintenant l'équation d'inconnue \(A\in \mathbb N^*\) afin de déduire les valeurs de \(A, B, C\) telles que le cycle existe. \[A=\frac{3A+1}{4}\iff 4A=3A+1\iff A=1\] Ainsi \(B=3A+1=3\times 1+1=4\;\) et \(C=\displaystyle \frac{B}{2}=\frac{4}{2}=2\)
Nous concluons donc que le seul cycle de longueur 3 existant est le cycle trivial.

Nous pourrions également nous demander s'il existe des cycles autre que le cycle trivial parmi ceux de longueurs différentes de 3. Essayons par exemple de chercher s'il existe un cycle de longueurs 5, toujours par l'absurde
Supposons \(A, B, C, D, E\in \mathbb N^*\) tel que \(A\lt B\lt C\lt D\lt E\) et \[A\to B\to C\to D\to E\to A\] Pas le même raisonnement que plus haut, on en déduit que \(B\) est pair et vaut \(3A+1\) et que \(C\) est impair et vaut \(\dfrac{B}{2}\)
Vu que \(C\lt D\), \(D\) est pair et vaut \(3C+1\) ; raisonnement identique pour trouver que \(E\) est pair et vaut \(\dfrac{D}{2}\)
Enfin, vu que \(E\to A\) et \(E\gt A\), \(A\) est impair et vaut \(\dfrac{E}{2}\). On résout donc l'équation suivante : \[A=\frac{\dfrac{3(3A+1)}{2}+1}{4}\iff 4A-1=\dfrac{9A+3}{2}\iff 8A-2=9A+3\iff -A=5\iff A=-5\] Or, nous avions supposé \(A\in \mathbb N^*\), ainsi l'équation ci-dessus ne possède aucune solution dans \(\mathbb N^*\) et \(\mathcal{S}=\emptyset\)
Nous avons donc démontré qu'il n'existe aucun cycle de longueur 5.
Plus généralement, le théorème de Eliahou nous dit qu'il n'existe aucun cycle de nombre positif inférieur à 180 000 000 000.

Approche algorithmique

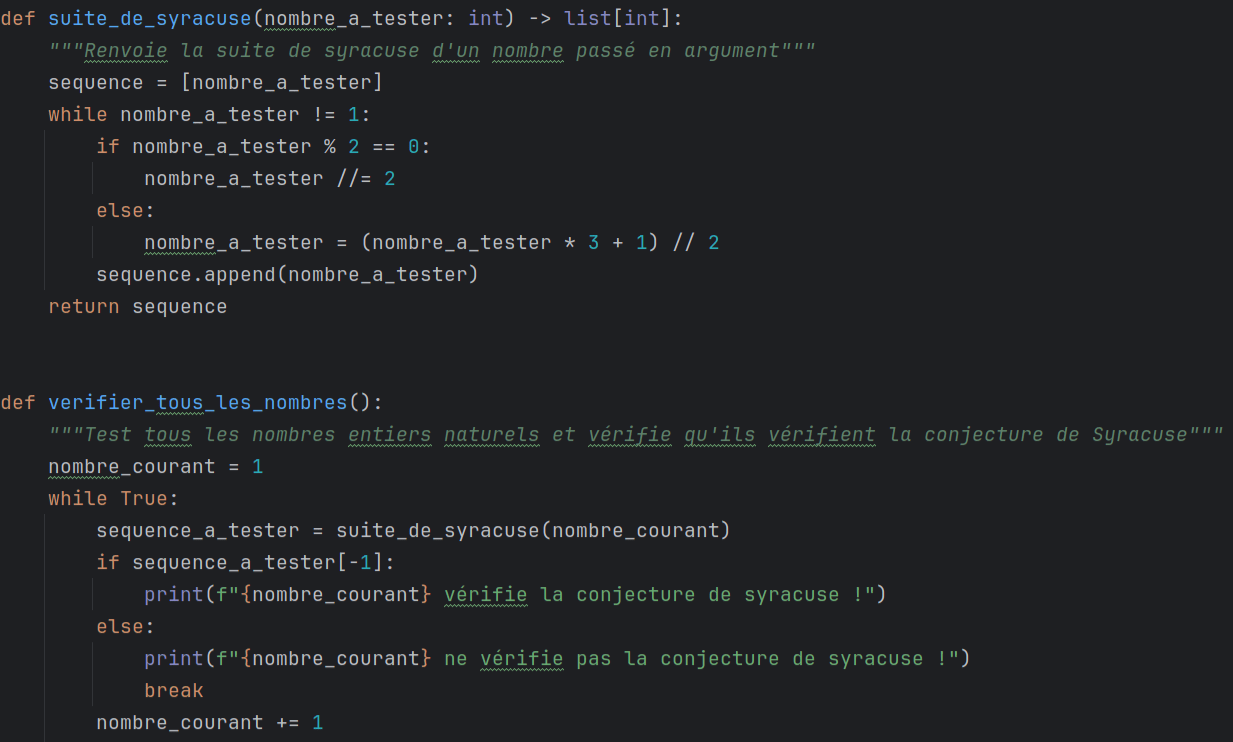
En se basant sur la définition explicite de la suite de Syracuse compressée, nous pouvons écrire une fonction python pour vérifier si tous les nombres entiers naturels vérifient la conjecture de Syracuse.
Le programme se découpe en deux fonctions :
- La fonction suite_de_syracuse() prenant en argument un nombre entier et retournant sa suite de Syracuse (compressée) sous la forme d'une liste d'entiers
- La fonction verifier_tous_les_nombres() qui est celle qui devra être appelée pour lancer le programme. Celle-ci utilise une boucle infinie pour tester un à un tous les nombres entiers en utilisant la première fonction. Dès qu'un nombre ne vérifie pas la conjecture, la boucle s'arrête grâce à l'instruction break

Notre algorithme précédant, bien que fonctionnel, est loin d'être le plus optimal. En effet, celui-ci teste tous les nombres entiers strictement supérieurs à 2. Pour disqualifier d'emblée certains nombres, nous pouvons modifier l'énoncé de la conjecture de Syracuse en un nouvel énoncé équivalent. Ainsi, nous pouvons affirmer que si tout entier a un temps de vol en altitude fini, alors tout vol atterrit. Cette nouvelle formulation est intéressante dans notre recherche de contre exemple car elle nous amène à ne chercher que des nombres dont la suite de Syracuse ne passe pas en dessous de \(u_0\). Nous pouvons donc disqualifier :

- Les nombres de la forme \(2n\) et \(2^n\), pour tout \(n\in \mathbb N^*\), car ceux ci sont directement divisés par 2 donc \(u_1 \lt N\)

- Les nombres de la forme \(4k+1\) car, \[4k+1 \rightarrow 12k+4 \rightarrow 6k+2 \rightarrow 3k+1\] et \(3k+1 \lt 4k+1 \iff u_3 \lt N\)
Les nombres de la forme \(4k+1\) atterissent donc.


- Les nombres de la forme \(16k+3\) car \[48k+10 \rightarrow 24k+5 \rightarrow 72k+16 \rightarrow 36k+8 \rightarrow 18k+4 \rightarrow 9k+2\] et \(9k+2 \lt 16k+3 \iff u_6 \lt N\)
Les nombres de la forme \(16k+3\) atterissent donc.

(Où \(\rightarrow\) désigne l'application de syracuse)

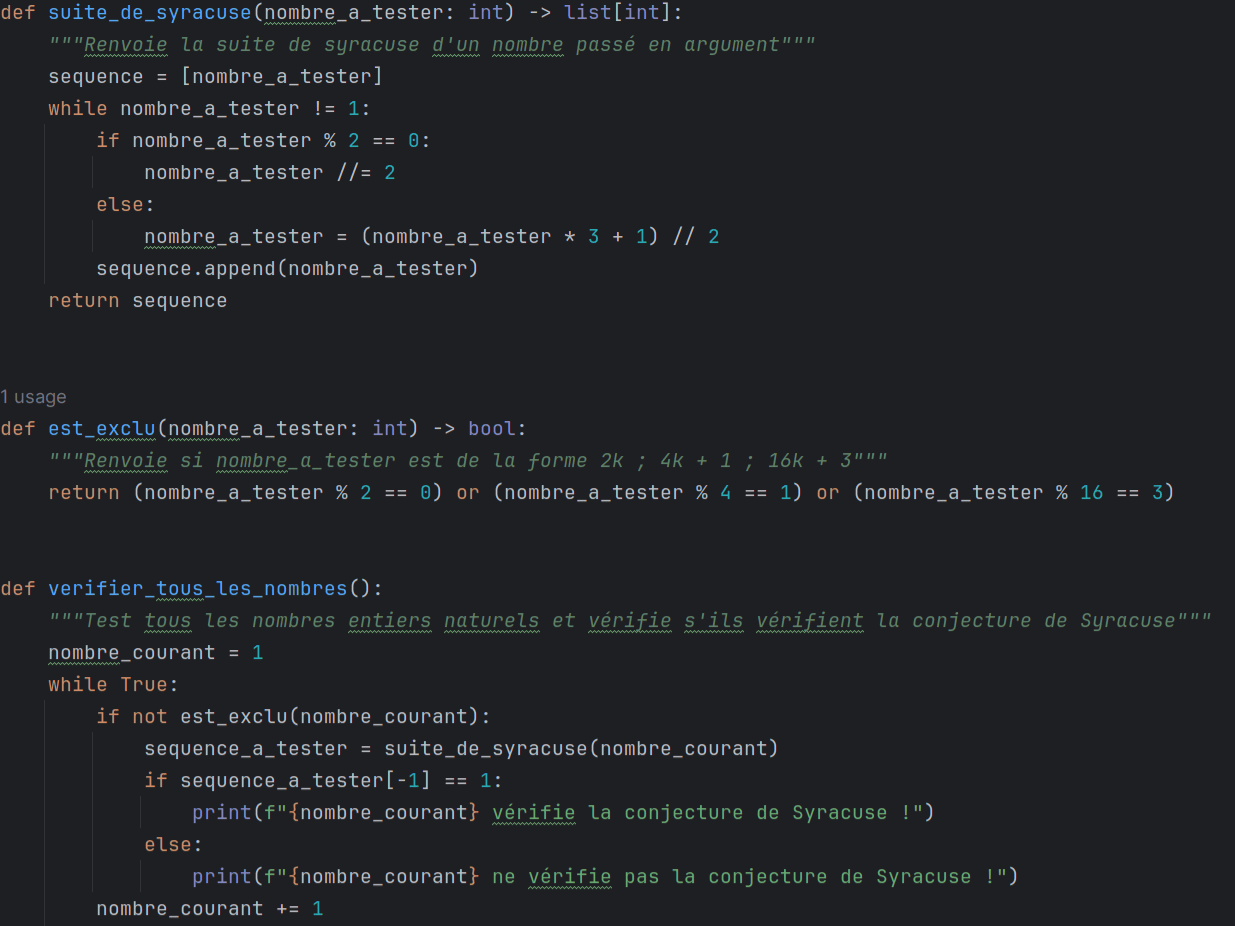
Par des calculs analogues, nous pouvons prouver que plus de 90% des nombres entiers naturels sont inutiles à tester car nous pouvons prouver que leur vol en altitude est fini. Ainsi, seuls les nombres impairs de la forme \(16k+7, 16k+11\) et \(16k+5\) peuvent être des prétendants à un contre exemple. En effet, nous ne pouvons pas prouver avec exactitude que ces vols atterissent car leur comportement varie en fonction des nombres.

Indice probabiliste

Nous parlerons ici d'indice probabiliste et non véritablement d'une approche à part entière car nos calculs et raisonnements ne seront pas des plus rigoureux. Le but de ce raisonnement est simplement d'aiguiller sur le sens de variation moyen de la suite de Syracuse d'un entier.
Tout d'abord, raisonnons sur la multiplication appliquée au nombre en fonction de sa parité. Par l'application de Syracuse : \[\forall n\in \mathbb N :\quad u_{n+1}= \left \{ \begin{array}{c @{=} c} \displaystyle \frac{1}{2}u_n & \text{Si } u_n \equiv 0[2] \\ \dfrac{3}{2}u_n & \text{Si } u_n \equiv 1[2] \end{array} \right. \] Avec \(N\in \mathbb N^*\quad ;\quad u_0=N\)
Nous négligeons ici le +1 lorsque \(u_n\) est impair pour simplifier les calculs.
Définissons maintenant deux évènements tels que : \[P:\, '\text{Le nombre est pair}'\quad ;\quad I:\, '\text{Le nombre est impair}'\] Trivialement, \(\mathbb P(P)=\mathbb P(I)=\frac{1}{2}\) car l'univers \(\Omega\) n'est composé que de ces deux élements
Ainsi, en moyenne, on multipliera successivement par \[\left(\frac{1}{2}\right)^{1/2}\times \left(\frac{3}{2}\right)^{1/2}=\sqrt{\frac{1}{2}}\times \sqrt{\frac{3}{2}}=\frac{\sqrt 3}{2}\approx 0.87 < 1\] Ce rapport nettement inférieur à 1 nous permet d'identifier un caractère plutot décroissant de la suite de Syracuse.
Cependant, Il n'existe aucune preuve rigoureuse de cette affirmation.

Extension sur Z

Depuis le début, nous utilisons la suite de Syracuse \(\left(u_n\right)_{n\in \mathbb N}\).
Cependant, quand est-il si nous considérions une suite définie pour tout \(N\) entier relatif différent de 0 ?
Pour y répondre, définissons une suite \(v_n\) telle que \[\forall n\in \mathbb N :\quad v_{n+1}= \left \{ \begin{array}{c @{=} c} \dfrac{v_n}{2} & \text{Si } v_n \equiv 0[2] \\ 3v_n+1 & \text{Si } v_n \equiv 1[2] \end{array} \right. \] Avec \(N\in \mathbb Z^*\quad ;\quad u_0=N\)
Suite à cette extension, plusieurs cycles différents du cycle trivial peuvent être observés :

• Avec \(v_0=-1, \quad u_1=3\times (-1)+1=-2 \quad ;\quad u_2=-\dfrac{2}{2}=-1=u_0\).
  Nous tombons donc dans un cycle \((-1, -2)\) de longueur 2
• Avec \(u_0=-5, \quad u_1=-14\quad ; \quad u_2=-7\quad ; \quad u_3=-20 \quad ; \quad u_4=-10\quad ; \quad u_5=u_0\)
  Nous tombons dans un cycle \((-5, -14, -7, -20, -10)\) de longueur 5
• Avec \(u_0=-17, \quad u_1=-50\quad ;\quad u_2=-25\quad ;\quad u_3=-74\quad \cdots\)
  Nous tombons dans un cycle de longueur 18

Il semble que, peut importe l'entier relatif \(N\ne 0\) choisi, celui-ci tombera dans un de ces trois cycles.
Cependant, rien n'a pour le moment encore été démontré.

Variante de la suite de Syracuse

Pour mieux appréhender le comportement de la suite de Syracuse, il peut être intéressant de s'intéresser à ses variantes.
Et si au lieu de multiplier par trois, nous multipliions par cinq
Définissons pour ceci une nouvelle suite \((u_n')_{n\in \mathbb N}\, \) et étudions la : \[\forall n\in \mathbb N :\quad u'_{n+1}= \left \{ \begin{array}{c @{=} c} \dfrac{u'_n}{2} & \text{Si } u'_n \equiv 0[2] \\ 5u'_n+1 & \text{Si } u'_n \equiv 1[2] \end{array} \right. \] Avec \(N'\in \mathbb N^*\quad ;\quad u'_0=N'\)
Comme lors de l'extension de \(u_n\) aux nombres relatifs, plusieurs cas peuvent être observés :

• Avec \(u'_0=6, \quad u'_1=3\quad ;\quad u'_2=16\quad ;\quad u'_3=8\quad ;\quad u'_4=4\quad ;\quad u'_5=2\quad ;\quad u'_5=1\quad ;\quad u'_6=6=u'_0\)
  Nous tombons dans le cycle \((6, 3, 16, 8, 4, 2, 1)\) de longueur 7.
• Avec \(u'_0=5, \quad u'_1=26\quad ;\quad u'_2=13\quad ;\quad \cdots \quad ;\quad u'_{10}=52\quad ;\quad u'_{11}=26=u'_1\)
  Nous tombons dans le cycle \((26, 13, 66, 33, 166, 83, 416, 208, 104, 52)\) de longueur 10, qui ne retombe jamais sur 1.
• Avec \(u'_0=7, \quad u'_1=36\quad ;\quad u'_2=18\quad ;\quad u'_3=9\quad ;\quad \cdots \quad ;\quad u'_{55}=208\, 604\quad ;\quad \cdots\)
  La suite grandit et boucle jamais, divergeant vers \(+\infty\).

En conclusion, lorsque l'on itère cette variante de l'application de Syracuse, tous les cas de figure se présentent : la suite peut boucler sur un cycle contenant 1, boucler sur un cycle ne contenant jamais un ou ne pas boucler et complètement diverger

Un énoncé indécidable ?

Après toutes ces tentatives infructueuses ou n'apportant pas une réponse claire et définitive quant à la validation ou à la réfutation de la conjecture, certains spécialistes viennent à se demander si cette question ne serait pas indescidable. Pour le moment, tous les nombres de l'intervalle \([1\, ;\, 2^{68}]\) vérifient la conjecture de Syracuse. Or, il est important de noter que, sur l'infinité des nombres naturels, ce nombre est ridiculement petit. A titre d'exemple, la conjecture de Pólya a été réfuté à l'aide d'un contre exemple estimé à \(1,845\times 10^{361}\).