1. Notion de vol
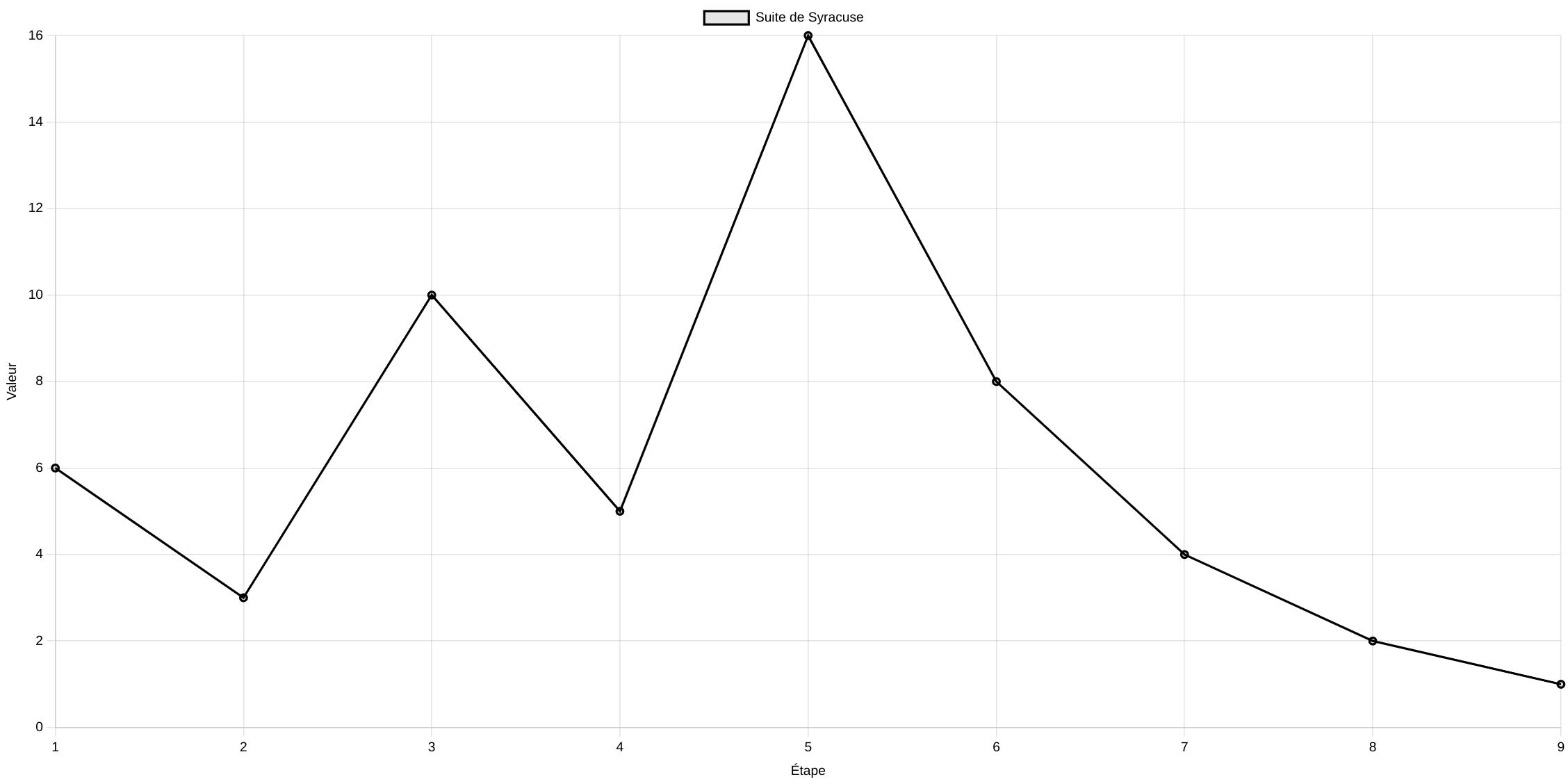
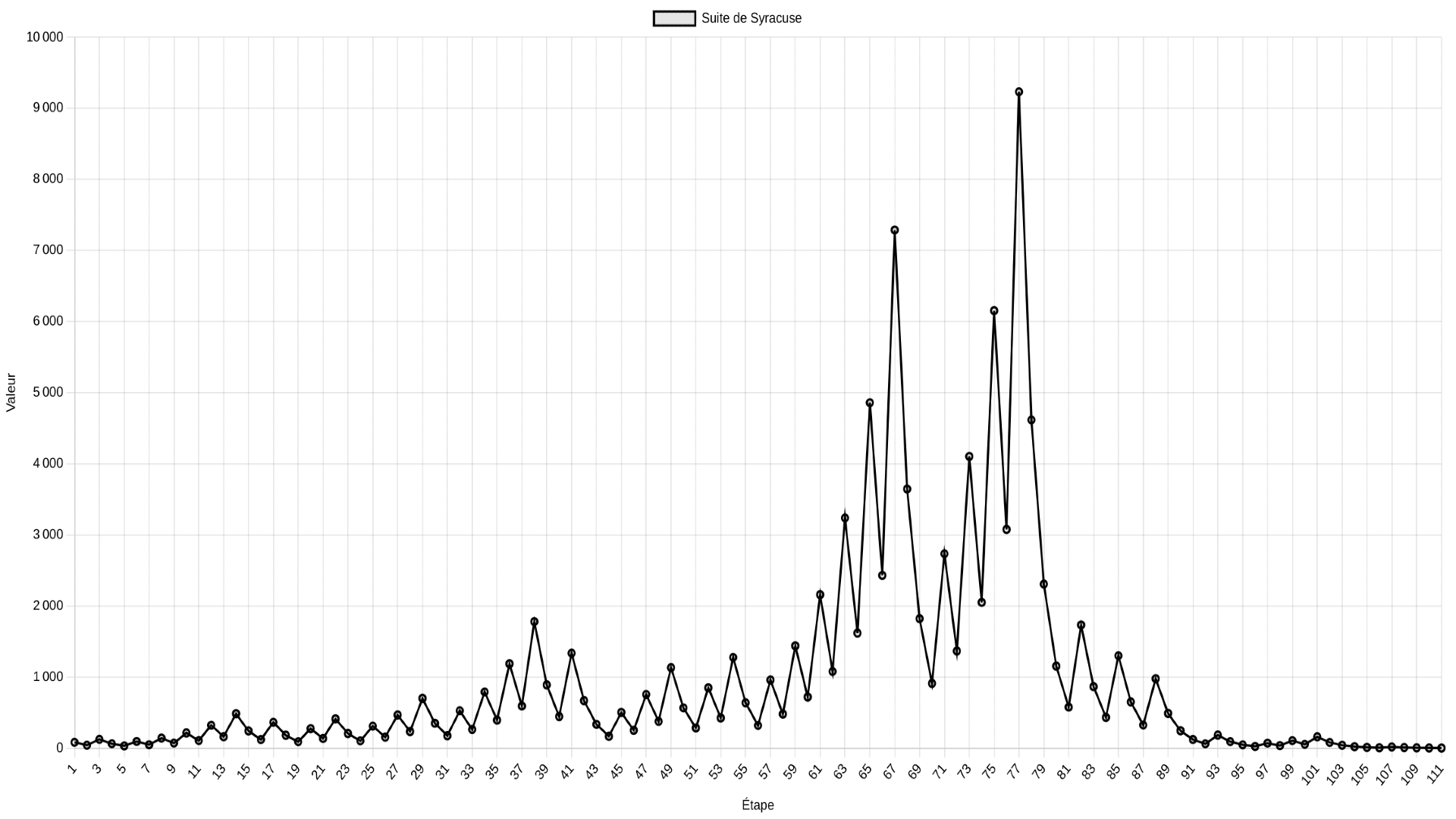
La notion de "vol" dans une suite de Syracuse est étroitement liée à sa représentation graphique. En effet, nous remarquons que ses valeurs peuvent atteindre des "hauteurs" considérables avant de redescendre plus ou moins rapidement. Cette trajectoire rappelle la course aléatoire d'une feuille emportée par le vent. C'est cette similitude qui a conduit à l'utilisation du terme "vol" pour décrire ce phénomène.
2. Temps de vol
Le temps de vol est défini comme le plus petit indice \(n\) tel que \(u_n=1\)
. En d'autre terme, le temps de vol d'une suite de Syracuse correspond au nombre d'itérations
effectuées jusqu'à ce que la suite atteigne 1 et, par conséquent, entre dans le cycle trivial.
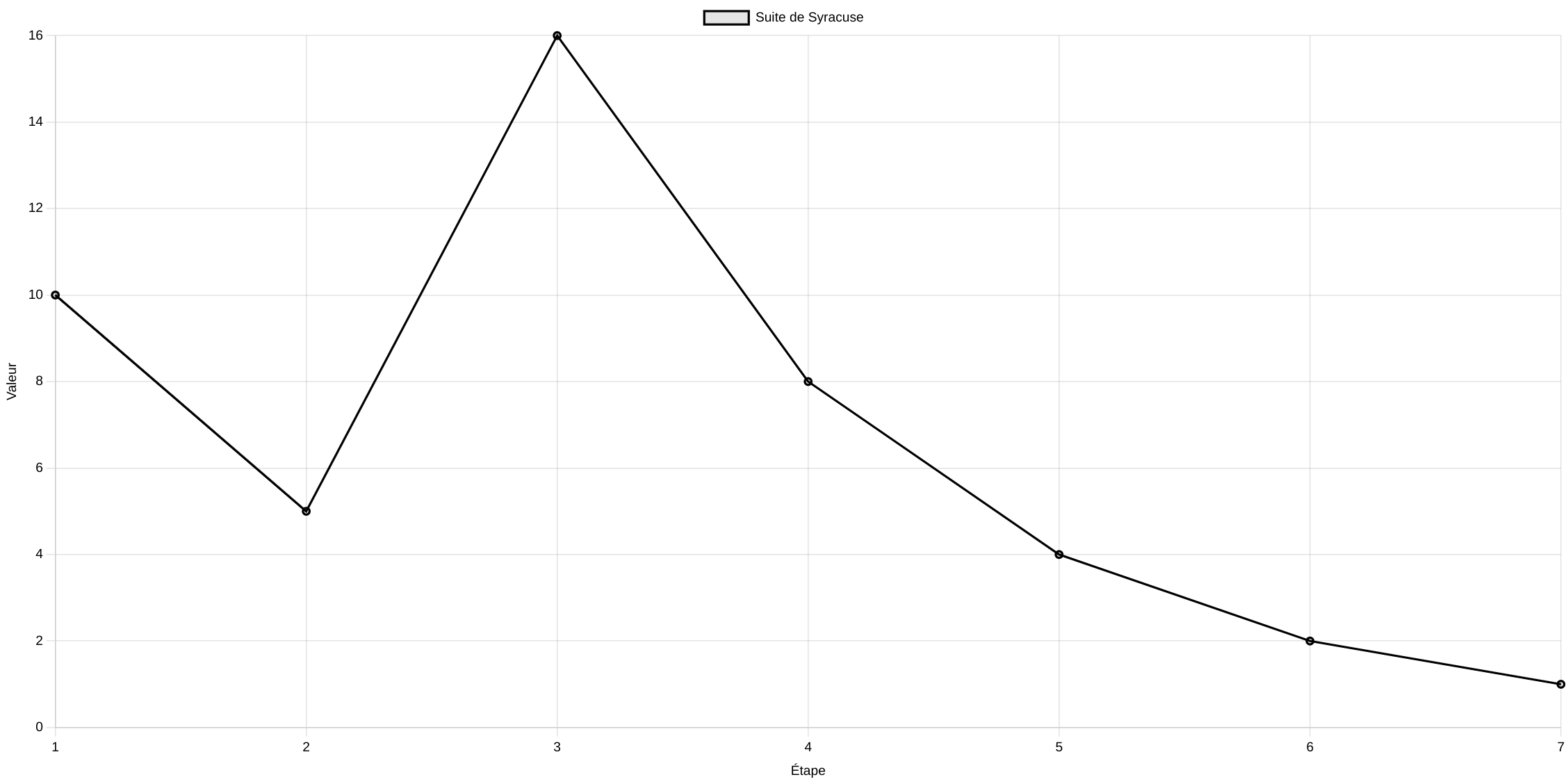
Exemple : La suite de Syracuse du nombre 20 a un temps de vol de 7 car il a fallu cette application
de Syracuse pour atteindre 1.
3. Altitude maximale
L'altitude maximale fait référence à la plus grande valeur atteinte au cours des itérations de la
suite.
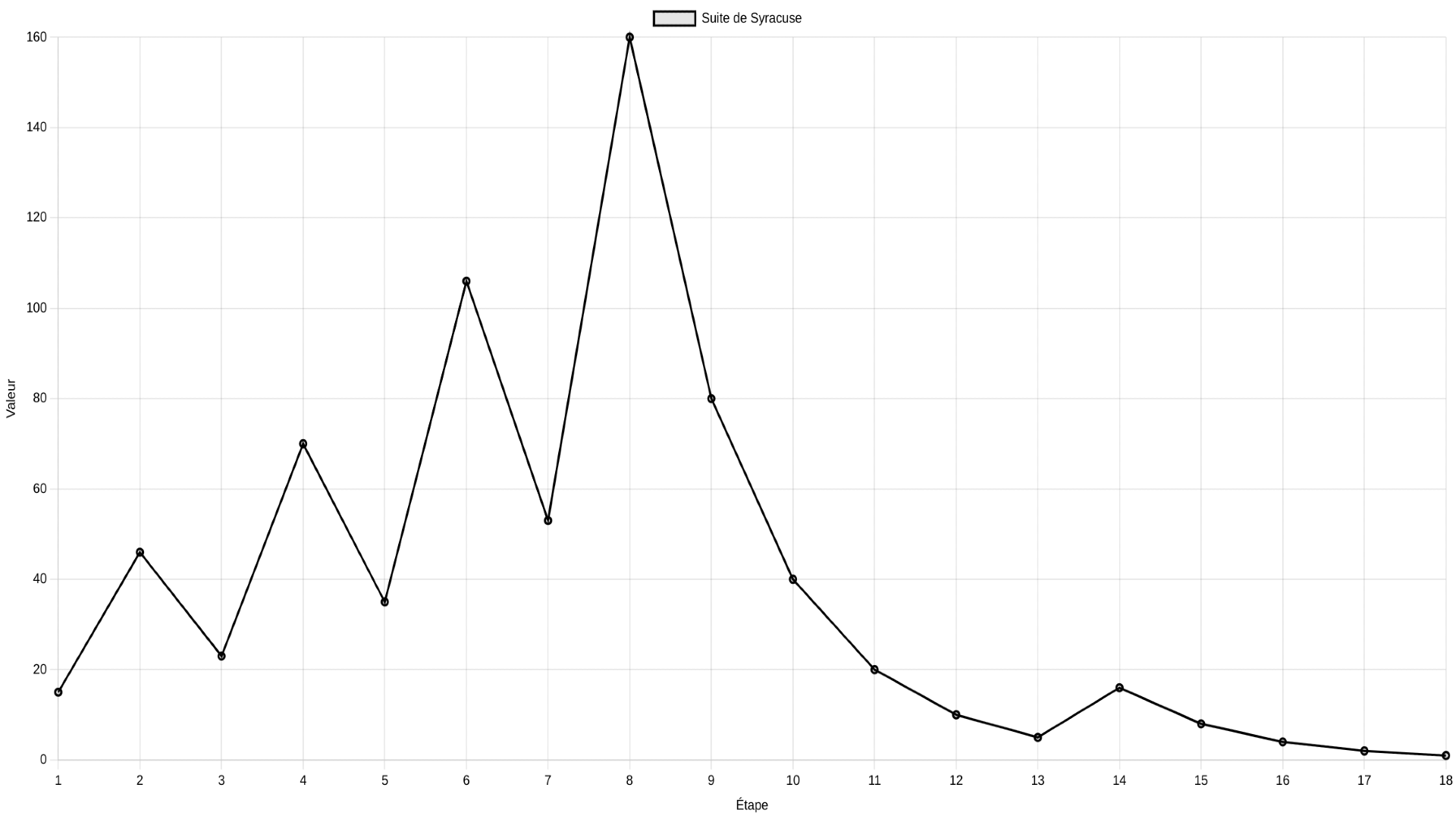
Exemple : Le maximum atteint par la suite de Syracuse du nombre 30 vaut 160.
4. Temps de vol en altitude
Le temps de vol en altitude d'un nombre est le plus petit indice \(n\) tel que \(u_{n+1} \lt u_n\).
Autrement dis, le temps de vol en altitude fait référence au nombre d'itération
nécessaire avant que \(u_{n+1}\) devienne plus petit que le nombre de départ.
Dans notre exemple, \(u_0=12\) et \(u_5 \gt u_0\) mais \(u_6 \lt u_0\)
Le vol en altitude de 12 vaut donc 6.