1. Approche algorithmique
En se basant sur la définition explicite de la suite de Syracuse compressée, nous pouvons écrire
une fonction python pour vérifier si tous les nombres entiers naturels vérifient la conjecture
de
Syracuse.
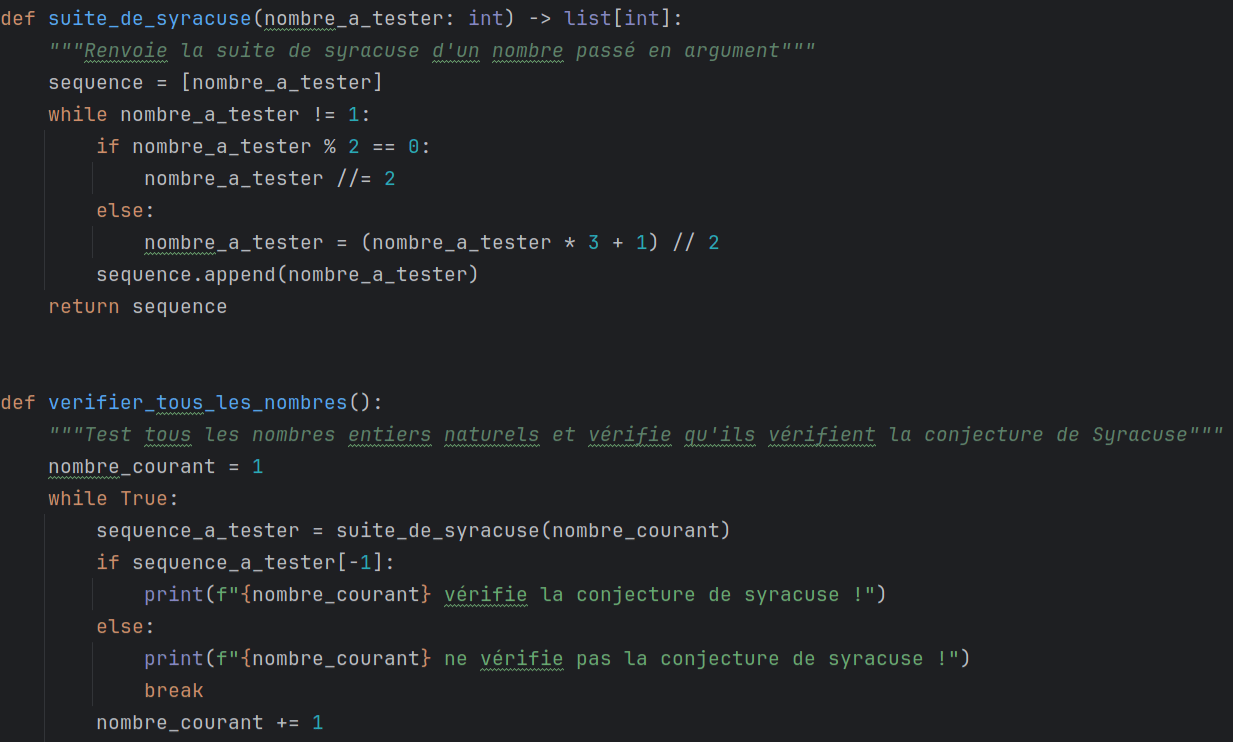
Le programme se découpe en deux fonctions :
- La fonction suite_de_syracuse() prenant en argument un nombre entier et
retournant sa suite de Syracuse (compressée) sous la forme d'une liste d'entier
- La fonction verifier_tous_les_nombres() qui est celle qui devra être appelée pour
lancer le programme.
Celle ci utilise une boucle infinie pour tester un à un tous les nombres entiers en utilisant la
première fonction. Dès qu'un nombre ne vérifie pas la conjecture, la boucle s'arrête grâce à
l'instruction break
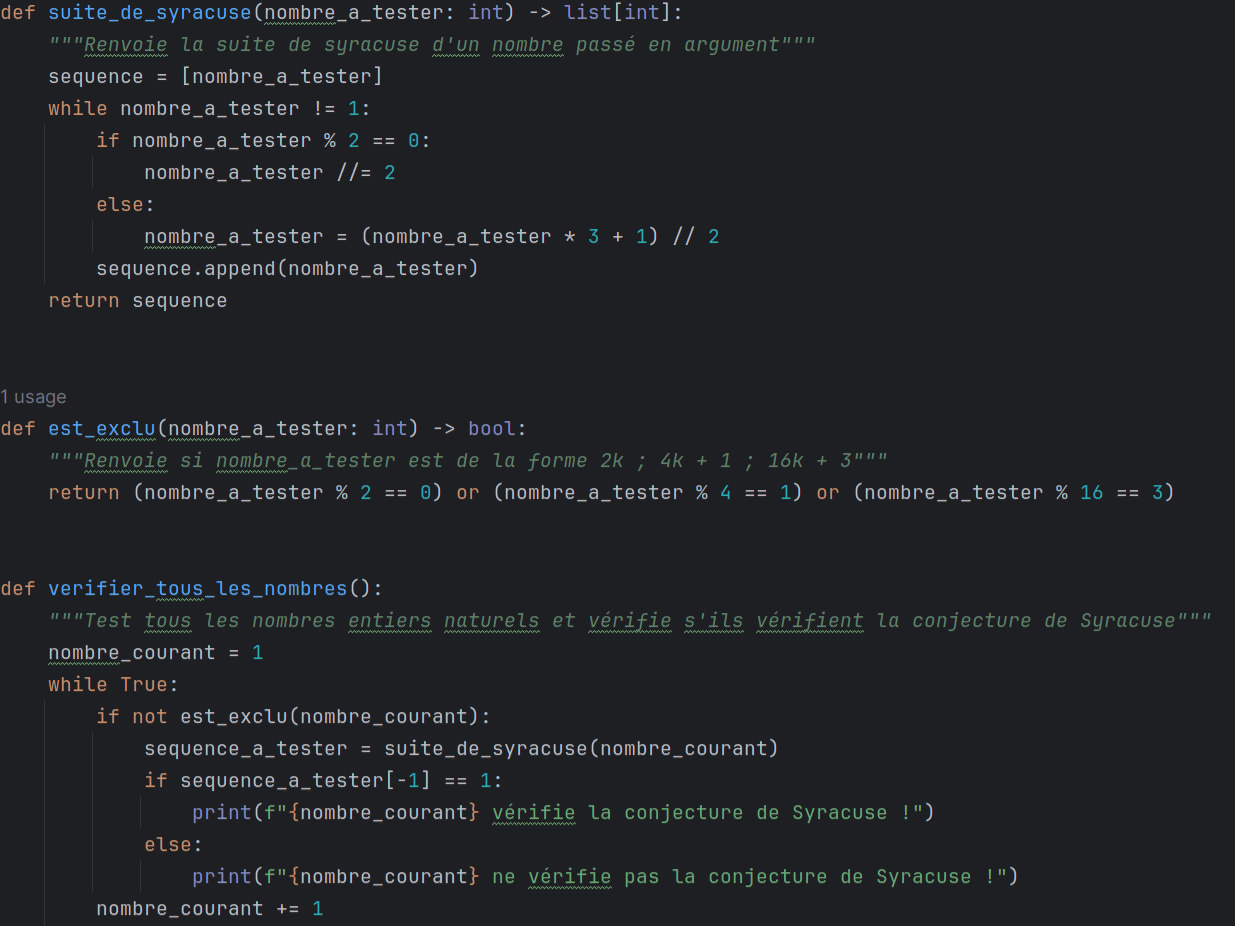
Notre algorithme précédant, bien que fonctionnel, est loin d'être le plus optimal. En effet, celui ci
teste tous les nombres entiers sctrictement supérieur à 2. Pour disqualifier
d'emblée certains
nombres, nous pouvons modifier l'énoncé de la conjecture de Syracuse en un nouvel énoncé
équivalent. Ainsi, nous pouvons affirmer que si tout entier a un temps de vol en altitude fini,
alors tout vol atterit. Cette nouvelle formulation est intéressante dans notre recherche de contre
exemple car elle nous amène à ne chercher que des nombres dont la suite de Syracuse ne passe pas en
dessous de \(u_0\) tels que :
- Les nombres de la forme \(2k\) et \(2^n\), pour tout \(n\in \mathbb N^*\),
car ceux ci sont directement divisés par 2 donc \(u_1 \lt N\)
- Les nombres impairs de la forme \(4k+1\) car,
\[4k+1 \rightarrow 12k+4 \rightarrow 6k+2 \rightarrow 3k+1\]
et \(3k+1 \lt 4k+1 \iff u_3 \lt N\)
Les nombres de la forme \(4k+1\) atterissent donc.
- Les nombres de la forme \(16k+3\) car
\[48k+10 \rightarrow 24k+5 \rightarrow 72k+16 \rightarrow 36k+8 \rightarrow 18k+4 \rightarrow
9k+2\]
et \(9k+2 \lt 16k+3 \iff u_6 \lt N\)
Les nombres de la forme \(16k+3\) atterissent donc.
(Où \(\rightarrow\) désigne l'application de syracuse)
Par des calculs analogues, nous prouvons prouver que plus de 90% des nombres entiers naturels sont inutiles à tester car nous prouvons prouver que leur vol en altitude est fini. Ainsi, seuls les nombres impairs de la forme \(16k+7, 16k+11\) et \(16k+5\) peuvent être des prétendants à un contre exemple. En effet, nous ne pouvons pas prouver avec exactitude que ces vols atterissent car leur comportement varie en fonction des nombres.
2. Recherche de cycles non triviaux
Une autre approche pour vaincre la conjecture de Syracuse serait de prouver qu'il existe un cycle
différent du cycle trivial.
Pour ce faire, raisonnons par l'absurde et admettons qu'il existe un autre cycle de longueur 3 \((A, B,
C)\) tel que
\(A\lt B\lt C\) et
\[A \rightarrow B \rightarrow C \rightarrow A\]
Nous avons donc nécessairrement \(A\) impair car, le cas échéant, \(B\) serait divisé par 2 et \(B\lt
A\).
Ainsi \(B=3A+1\), qui est pair donc \(C=\frac{B}{2}=\frac{3A+1}{2}\). Puisque \(C \to A\) et \(C \gt
A\), \(C\) est pair et vaut
\(\frac{B}{2}=\frac{1}{2}(\frac{3A+1}{2})=\frac{3A+1}{4}\)
Résolvons maintenant l'équation d'inconnue \(A\in \mathbb N^*\) afin de déduire les valeurs de \(A, B,
C\) tels que le cycle existe.
\[A=\frac{3A+1}{4}\iff 4A=3A+1\iff A=1\]
Ainsi \(B=3\times 1+1=4\;\) et \(C=\frac{B}{2}=\frac{4}{2}=2\)
Nous concluons donc que le seul cycle de longueur 3 existant est le cycle trivial.
Par des méthodes de démonstration par l'absurde, il est possible de prouver
qu'il n'existe pas de cycle de longueur 2 ou 5.
En général, le théorème de Eliahou nous dit qu'il
n'existe aucun cycle de nombre positif inférieur à 180 000 000 000.
Approche inverse : arbre de Syracuse
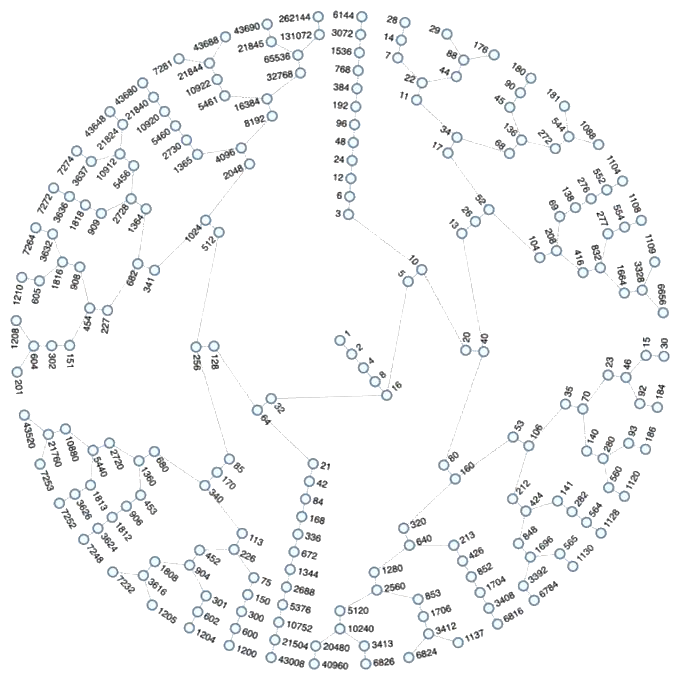
Depuis le début, nos approches sont similaires. Nous partons d'une itération sur l'application de Syracuse pour en observer ou démontrer des propriétés. Une autre approche possible est de changer de point de vue et de prendre le problème à l'envers. C'est de cette idée qu'est née l'arbre de syracuse.
Partons de 8 Pour y arriver, nous venons soit de l'application de Syracuse 3x + 1, soit de
\(\frac x 2\).
On test de résoudre l'équation d'inconnue \(n\in \mathbb N^*\) :
\[3n+1=8\iff 3n=7\iff n=\frac{7}{3} \notin \mathbb N^*\]
On en déduit donc que 8 ne vient pas de l'application de Syracuse sur les nombres impairs car
\(\frac{7}{3}\) n'est pas un entier naturel. Ainsi, 8 vient forcément de l'application de
Syracuse sur les
nombres pairs et donc de 16.
Nous passons maintenant à 16. Par la même méthode que pour 8, on résoud les équations
d'inconnues \(n\in \mathbb N^*\) :
\[3n+1=16\iff n=5\in \mathbb N^*\, \, \, \text{ou}\, \frac{n}{2}=16\iff n=32\in \mathbb N^* \]
Ces deux équations possèdent des solutions naturels, l'arbre de Syracuse possède donc 2 branches
qui représente les 2 applications de Syracuse possibles. À partir de ces deux branches, d'autres
seront à leur tour crées. Ainsi, il est dit que tous les nombres entiers naturels sctrictement
positifs sont présents dans cet arbre. Nous n'avons cependant par encore réussi à le démontrer.
Un énoncé indécidable ?
Après toutes ces tentatives infructueuses ou n'apportant pas une réponse claire et définitive quant à la validation ou à la réfutation de la conjecture, certains spécialités viennent à se demander si cette question ne serait pas indescidable. Cependant, une méthode de résoudre cette conjecture serait de trouver un contre exemple à celle ci. Pour le moment, tous les nombres de l'intervalle \([1, 2^{68}]\) vérifient la conjecture de Syracuse. Or, il est important de noter que, sur l'infinité des nombres naturels, ce nombre est ridiculement petit. A titre d'exemple, la conjecture de Pólya a été réfuté à l'aide d'un contre exemple estimé à \(1,845\times 10^{361}\).